Someone once said that the study of Hydrology and Hydraulics is one part art, the rest part voodoo. Hydraulics is so much more an empirical study or relationship than pure voodoo. I am glad I am not the only one out on a rainy day watching the water rise in the streams, channels and in the backyard sandbox.
This being a week before the great Irish celebration and the week of the IAFSM annual conference, I will dedicate this post to Manning. No, not Eli or Peyton, but Robert Manning, the District Engineer Engineer of the Arterial Drainage Division of the Irish Office of Public Works. Sounds like a roadtrip is in order to origins of formula…
As we know from our earlier 101 posts about the Rational Equation, we have solved for the runoff peak flow, or Q.
How do we solve for either the depth of flow or the velocity? Well, one not need to look too much beyond the Discharge formula :
and Manning Formula
Rh is Hydraulic Radius (ft, m). K is equal to 1 for SI Units, and 1.486 for Imperial units. S is the Slope in ft/ft or m/m.
so that for open-flow channels, where wetted perimeter is the sum of the li or the length of contact the water has with a friction surface like a pipe or streambed. This is a simple calculation if this is a box, but can get a little more complicated in a round pipe.
None the less, combining the Discharge formula and the Manning equation, we can arrive at:
AutoCAD Civil 3d Hydraflow Express Extension tools uses the Mannings equation to solve the following possible channel types
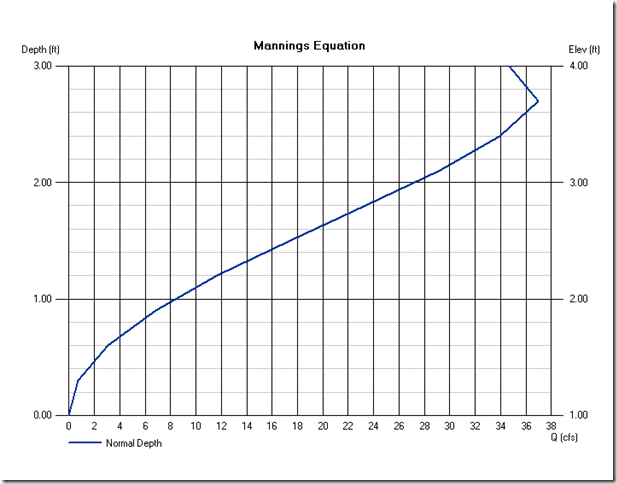
 to arrive at a nice Normal Depth Curve.
to arrive at a nice Normal Depth Curve.
Mannings equation is used to ultimately arrive or rather derive a number of other hydraulic equations including the SCS TR55 method of calculating the time of concentration.
[Editors note: The post was supposed to appear last week..]

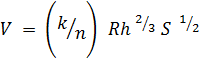
![clip_image002[13]](http://www.civil4d.com/wp-content/uploads/2009/03/clip-image00213-thumb.gif)
![clip_image002[15]](http://www.civil4d.com/wp-content/uploads/2009/03/clip-image00215-thumb.gif)