In my first post in this new Engineering 101 series, I talked about determining runoff rates (Q) using the Rational Method. That post ended like any good summer blockbuster, leaving open the possibility for a sequel. We’ll, unlike the years you spent waiting for the new Batman sequel, this next post in Rational Method Saga arrives only a couple weeks after the first post (sorry, I was our of town last week!).

When we left off, we had explained the the runoff rate Q is equal to c i A, where c is the runoff coefficient, A is the tributary area, and i in the rainfall intensity. We also discussed how c and A were determined. In this post, we’ll discuss one of the main components of determining i, the Time of Concentration, or Tc.

As the term implies, Time of Concentration (from here on out, Tc) is the time it takes for runoff to reach its maximum flow rate. What this means in plain English is that Tc is the time it takes for the runoff from a given area to reach the greatest rate it will ever reach during a storm.

Imagine you’re standing on a paved road at the bottom of a hill and a rain shower starts. Imagine further a “piece” of water, one raindrop, falls on the road 10 feet from you. You’re holding a stopwatch and as soon as the raindrop hits the pavement 10 feet from away, you start the stopwatch and time how long it takes to get to you. If the pavement is sloping evenly, any raindrop that falls on the road 10′ from where you are will reach you at the same time. Similarly, if you timed how long it takes for a raindrop that hits the pavement 20′ away to reach you, not only will that rain drop get to you, but so will all the rain drops 10′ away, and 5′ away, 1′ away and so on. So as you can see, to clock the Tc for maximum flow rate, we need to find the raindrop that falls the farthest away from where you are standing, and that will still flow to where you are; in our case, the top of the hill. The amount of water splashing around your feet after the time it takes a raindrop that lands on the road at the top of the hill to reach you will include all the rest of the water running between you and the top of the hill.

Thus, Tc is the time it takes for a piece of water to travel from the farthest point in a watershed or “catchment” (the area of which is A, discussed in the last post), and all the water in between you and the farthest point, to the point of concentration, which could be an inlet or detention basin or outlet swale.

So with an understanding of what Tc is, we can move on to discussing how it is calculated. There are several methods for calculating Tc, but we’ll look at just one in this post. The National Resource Conservation (NRCS, formerly the Soils Conservation Services, or SCS) is the organization behind the wildly popular TR-55 and TR-20 computer applications used in hydrologic analysis around the U.S. and they provide a very common method for calculating Tc. We’ll examine this method.

The NRCS provides a Tc worksheet that breaks the runoff into three distinct components. These components include Sheet Flow, which applies to to up to the first 100′ of flow length (some sources assume Sheet Flow occurs for up to 300′); Shallow Concentrated Flow, which applies to the flow state after the initial 100′ (or 300′) up to 1,200′ ; and Channel Flow, which applies to any flow occurring after 1200′.

Let’s look at each one of these components in turn. (You may want to print out the worksheet to make it easier to follow along.)

Sheet Flow:

Sheet flow is calculated from four variables:

• Manning’s roughness coefficient, n (dimensionless)
• Flow length, L (feet)
• Land Slope, s (feet/feet)
• Two-year 24-hour rainfall, P2, (inches)

With these variables, Tc (hours) for Sheet Flow is then calculated using basic algebra as:

Tc = [0.007 x (nL)^0.8] / [P2^0.5 x s^0.4]

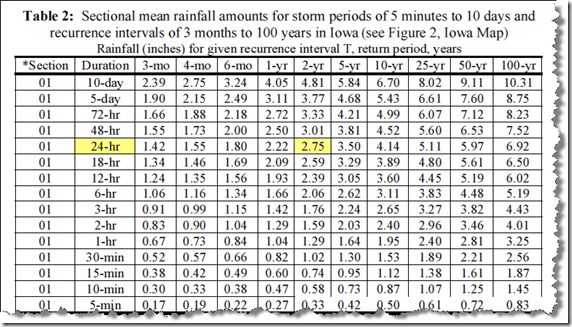
So how are the input variables determined? Manning’s coefficient and Rainfall Intensity are obtained from published data. For example, NRCS publishes Table 3-1 that contains n values for various surface descriptions.

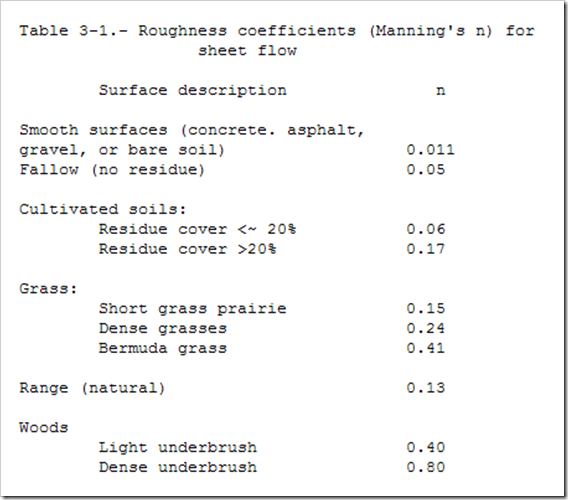
Rainfall intensities are also published for most regions in the U.S. For example, the following image shows the intensities for an section of Iowa. As you can see from the highlighted values, the 2-year, 24-hour intensity for this particular region of Iowa is 2.75 inches. It is important to note that intensities can vary widely over relatively small distances so be sure the table you have is specific to the area in question.

Slope and length are determined by examining the existing topography. In Civil 3D, there are many tools that can help you obtain this information. Examine the Surface > Utilities menu for the Waterdrop function that will give you a flow path polyline. Use Divide tools to place ticks every 100′ on the resultant polyline and then use Inquiry tools to get slope. After determining the Sheet Flow component, you can move on to Shallow Concentrated Flow.

Shallow Concentrated Flow:

Shallow concentrated flow is a little easier to calculate that Sheet Flow. It too relies on four variables:

• Surface description (paved or unpaved)
• Flow Length, L (feet)
• Watercourse slope, s (ft/ft)
• Average velocity, V (ft/second)

With these variables, Tc (hours) for Shallow Concentrated flow is then calculated using basic algebra as:

Tc = L / [3600 x V]

Slope and length can be determined in a similar manner as used for Sheet Flow. Surface description is easy enough to determine (is it paved? yes or no). With slope and surface description, you can then refer to NCRS Figure  3-1 to determine Average Velocity.

In the following example, assume a slope of 0.16 on an unpaved surface. From the curves, the Average Velocity is 6.5ft/second.

The final component is calculated for flow that has become channelized.

Channel Flow:

The equation for calculating Tc for channel flow is identical to that used for calculating Shallow Concentrated Flow. The difference is in the way the variable inputs are calculated. In a nutshell, we use the very popular Manning’s equation to determine V.

V = [(1.49) x (r^.667) x (s^0.5)] / n

This is the same equation used in sizing storm sewer pipes and we’ll cover it in detail in another posting.

Summing it Up:

After you’ve determined the times for each of the components contributing to overall flow, simply add them together to get your overall Tc. The minimum Tc used in TR-55 is 0.1 hours and the shorter the Tc, the greater the rainfall intensity. Of course, after you go through all this work, the reviewing agency will tell you to use a Tc of 10 minutes!

So how does Tc help us know the value of intensity, i ? Well, with Tc, we can look up intensity in a table similar to the one we we used to determine P2 above (but that lists intensity as inches/hour). Let’s say that after all these Tc calcs, we determine that Tc = 15 minutes. Let’s further say that we’re interested in the runoff rate for a 100-year storm in Section 01 of Iowa. From the table we see that i = 1.87 inches which, for 15 minutes is 7.48 inches/hour (not shown in table). We now know c, i, and A and can thus determine Q.

Enjoy!

Additional Resources: Here is a great write up that says the same thing in more detail in less words.